单级齿轮减速机双重优化设计方法
摘 要:齿轮基本参数的选择是齿轮设计中的一项非常重要的内容&传统的齿轮设计方法忽视了所选择的基本参数对啮合效率的影响,从而造成了能源浪费和经济损失&首先从减少体积出发对圆柱齿轮结构参数进行优化,然后在此结构参数的基础上,基于啮合效率,进行再次优化,得到既减少体积又提高啮合效率的系列结构参数.
关键词:齿轮设计;齿轮基本参数;啮合效率;双重优化
1 引言
优化设计是一种现代设计方法,建立在最优化数学理论和现代计算机技术的基础之上,其任务在于运用计算机自动确定工程设计的最优方案&优化设计方法应用于机械设计中,可以提高产品质量,降低产品成本,是一种具有重要经济意义和巨大应用潜力的先进技术.
圆柱齿轮结构参数优化通常从减少体积'减少轴距的角度对齿轮的结构参数进行优化设计,这种设计方法以满足强度’寿命理论为准则,取得了较好的优化效果,特别是相关行业软件和数
学工具的推广,使这些优化工作变得规范,操作简单,在实际设计中得到广泛的应用.
降耗节能是国民经济可持续发展的重要任务之一,所以效率的高低是衡量机械性能的一个重要指标&上述设计方法,忽视了所选择的参数对啮合效率的影响,从而造成了能源浪费和经济损失.
啮合效率是反映齿轮传动的工作效率的一个重要指标&因此,提出一种双重优化的齿轮设计优化方法,即,首先从减少体积或轴距的角度对齿轮的结构参数进行优化,在此基础上,再从啮合效率的角度对齿轮的设计参数进行再优化&提出设计既满足强度’寿命要求,又具有传动效率高特点的齿轮设计的通用方法.
第二部分对以减少体积或轴距为目标的齿轮设计优化方法进行简单介绍&第三’四部分对齿轮啮合效率的计算’以啮合效率为目标的齿轮设计优化方法进行详细介绍.
2 基于强度 寿命准则的优化方法
从目标函数建立’约束条件确定’优化方法选择三方面简要介绍基于强度’寿命准则的优化设计的过程与步骤.
2.1 目标函数的建立
单级齿轮减速器的结构简图,如图 < 所示,轴板孔数为 @&已知输入功率 ?A8=%BC,输入转速 *<A<%%%DEF+,,齿数比 9AG,齿轮的许用接触应力[!]@A=GGHI1,主动齿轮的许用弯曲应力[!];A8"<HI1,从动齿轮的许用弯曲应力[!];A8<9HI1&求在满足零件强度和刚度条件下,使减速器体积最小的各项设计参数&由于齿轮和轴的尺寸(即壳体内的零件)是决定减速器体积的依据,因此可按它们的体积之和最小的原则来建立目标函数.
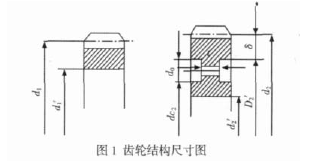
输入、输出轴 A<$’A8$近似看成直径一样粗(即计算应力时,不考虑其阶梯部分)&设大小齿轮的齿宽均为 B,轴支承跨距为 C,轴向尺寸为:CJ$=KF,CJ9$KF,齿数 DED<&根据齿轮几何尺寸及齿轮结构尺寸的计算公式,壳体内齿轮和轴的体积可近似表示为: 
2.2 约束条件的确定
单级圆柱齿轮结构参数优化是一个 / 设计变量,#/ 个约束条件的优化设计经典问题&其设计约束根据最小齿数’齿宽系数’模数限制’齿轮直径’轴径’轴支撑’接触疲劳强度’弯曲疲劳强度’主动轴刚度’主动轴弯曲强度等确立&由于单级圆柱齿轮结构优化是个优化设计的经典问题,相关文献有详细介绍,不再赘叙&仅列出最终约束条件

2.3 选择优化方法
这是一个带有 #/ 个约束的 / 维优化设计问题,通过采用复合形法来进行优化计算&复合形法的基本原理是:在可行区域内选取 2 个设计点作为初始复合形的顶点,通常取 34##2$&3&
比较这些顶点的目标函数值,其中目标函数最大的点为坏点,以坏点之外其余各点的中心为映射中心,寻找坏点的反射点,一般反射点总是优于坏点,然后以反射点代替坏点,构成新的复合形&依此步骤重复多次,使复合形的位置越来越靠近最优点,最后输出复合形中目标函数最小的点作为近似最优点。
基于 345647 的优化函数,把目标函数和约束条件分别定义为 3 文件,通过 345647 的有约束优化函数 89:;<=; 进行优化计算,最终得出优化变量

3 啮合效率的计算
3.1齿轮传动瞬时啮合效率的计算
如图 2 所示,设两轮廓 #’& 在点 5 接触,其中 3’3 为两轮廓在点 5 的公法线,6#’6&为两轮廓在点 5 处的速度,"#’"&为 6#’6&与公法线 3’3 的夹角,两轮廓总反力 /#&’/&#与公法线 3’3 的夹角为#,设 # 为主动件&压力角与啮合点坐标 > 的关系图,如图 3 所示.
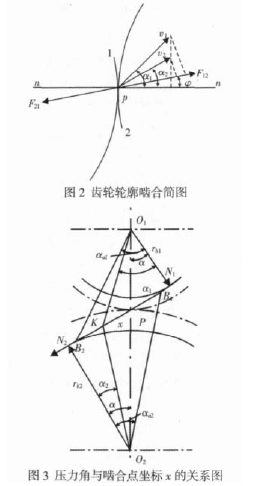
则点 5 处驱动力的功率:7?!/#&"6#"<=@("#%#)点 5 处克服工作阻力所需的功率7&!/#&"6&"<=@("&%#)&由 /#&#/&#,以及根据平面啮合的基本定理,两齿轮在接触点的速度沿公共法线方向的分量相等,即 6#<=@"#!6&<=@"&&因此点 5 处的效率:
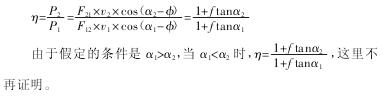
3.2 齿轮传动平均啮合效率的计算
上面求出了齿轮副的瞬时啮合效率,其值随着啮合点的变化而变化,因此需要用积分求出平均啮合效率&如图 ! 所示,!"!#为实际啮合线,在节点 " 的两侧,! 具有不同的表达式,因此采用分段积分&其中,


4 基于啮合效率的齿轮设计再优化方法
4.1 目标函数的建立
齿轮的基本参数为齿数 *’模数 )’压力角"’齿顶高系数-%和顶隙系数 2&由平均啮合效率公式可以看出,式中不包含 )’2,此这里就不予讨论;虽然 ! 求解公式中包含 -%,但由于 -%已经标准化,这里也不再讨论&由于 *,和 +,#在第一步优化中已经确定,这里不再讨论,而且,*,和 +,#对啮合效率的影响比较小,详细论证见参考文献,这里不再论述&因此,在第二步优中,仅考虑压力角 "以及摩擦系数 , 对啮合效率 ! 的影响。
在平均啮合效率公式,取 &,$",&#$ ,,即可建立目标函数:3(4)56(&,,&#)& 4.2 约束条件的确定:

4.3 选择优化方法

从优化结果可以看出,适当增加压力角,有利于啮合效率的提高,但达到一定程度后,啮合效率反而下降;摩擦系数与啮合效率成反比关系。
5 结论
首先从减少体积出发对圆柱齿轮结构参数进行优化,然后在此结构参数的基础上,基于啮合效率,进行再次优化,得到既能减少体积又能提高啮合效率的系列结构参数。
传统的齿轮设计忽视了所选择的基本参数对啮合效率的影响,从而造成了能源浪费和经济损失&从优化结果可以看出,在齿轮设计中,其基本参数的选择在满足强度’寿命的前提下,应考虑选择合理的压力角,同时应尽量减小摩擦系数。
优化设计方法应用于机械设计中,可以提高产品质量,降低产品成本,是一种具有重要经济意义和巨大应用潜力的先进技术&减速机作为机械传动中机械变速的关键部件,其优化设计要求在保证产品品质的同时,实现最小体积’最大效率的目标,是一个典型的多目标优化问题&基于 =&%2&; 的优化函数使优化工作简单易行。









