摆线针轮行星传动的运动平稳性分析
摘要:分析了摆线轮有加工误差或修正的齿廓与针轮针齿的啮合的关系,建立了摆线针轮行星传动瞬时传动比的计算式。根据计算所得的瞬时传动比变化曲线可看出,这种传动因加工误差或齿廓修正将导致传动出现运动不平稳性,所作分析将为改善摆线针轮传动的啮合特性提供了参考。
齿轮传动是工程中应用最广泛的一种机械传动。在齿轮传动中,通常采用渐开线、摆线和圆等曲线作为齿廓曲线,最广泛采用的齿廓是渐开线齿廓。渐开线齿廓的最大特征是无论齿廓曲线形状如何变化,只要其为渐开线齿形,任何一对这样的轮齿啮合均共轭,其传动比均为恒定值。因此渐开线齿轮传递运动平稳,故渐开线齿轮传动被广泛使用.
摆线针轮行星传动具有传动比大、体积小、重量轻,以及高的传动效率和过载能力等优点,现在也被广泛的使用。在摆线针齿啮合的传动中,在理论上一个特定直径的针齿只与一特定条件的
变幅摆线共轭,当针齿直径改变、偏心距变化,或变幅摆线有改变,均会破坏其共轭关系,使其传动比不再恒定。实际使用摆线针轮行星减速机,由于有加工误差或因齿廓修形等原因,很难做到针齿和摆线齿的共轭。鉴于以上情况,对于摆线针齿啮合的齿轮传动,由于加工误差或因齿廓修形引起传动比的变化,产生的运动不平稳性,是很值得重视和研究的。以下主要分析摆线轮齿形误差对传动的影响。
1 摆线针轮的啮合关系分析
在摆线针轮行星传动中,假定针齿直径和针齿分布圆直径均为理想值;两轮中心距为理论中心距。为了使啮合轮齿获得一定的顶隙和侧隙,在摆线轮加工中,常采用移距修正和等距修正法。经修正的摆线轮与针轮针齿啮合时,已不是理想的共轭齿廓啮合,则必然会导致传动比发生变化,引起运动的不平稳性。在图1所示的轮齿啮合中,理想的针齿圆与理想的共轭摆线轮齿廓曲线C在M点接触啮合,此理想的摆线轮齿廓C的曲线方程为〔1〕:

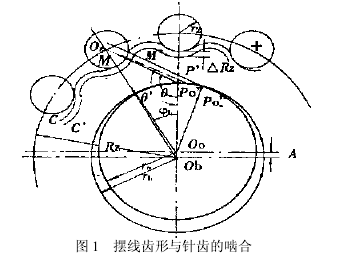
理想啮合时接触点M的公法线与两轮连心线交于P点,根据齿廓啮合基本定律〔2〕,其传动比为:
![]()
但在实际传动中,由于有加工误差或进行修正,此针齿外圆将与实际齿廓曲线C′上的M′点接触啮合。此时过接触点的公法线(图中虚线OzPa′)将与两轮连心线交于P′点,则其传动比为:
![]()
存在有加工误差或进行齿廓修形的实际摆线齿廓曲线C′的方程式为〔1〕:
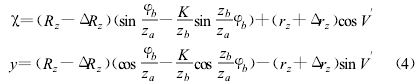
式中:ΔRz为移距修正量,Δrz为等距修正量,K′为移距修正时的齿廓变幅系数;
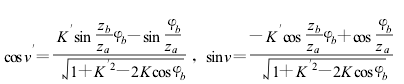
根据啮合关系和齿廓的曲线方程,可以确定出与此针齿啮合的齿廓曲线C′上的M′点,并可确定出M′点的法线M′P″a和M′为接触点时对应的θ'角(过接触点的法线与两轮连心线的夹角),由正弦定理则有:

2 瞬时传动比的计算
由以上齿廓曲线方程式和轮齿啮合的几何关系,编程并利用计算机求解,即可计算出摆线针轮行星传动的瞬时传动比。选取理论传动比为iHa=29,Rz=110mm,a=2mm,rz=7mm的机型。并选取不同的修正量■Rz,经计算得出单对齿啮合的瞬时传动比iHa'随啮合转角φb的变化曲线如图2所示。由图可见,随着修正量的增大,单对齿啮合的瞬时传动比变化增大,在修正量■Rz<0.05mm时,在较大的啮合区间,传动比iHa'接近于理论值(图中曲线1);当加工误差或修正量为■Rz=0.30mm时,只在很小的范围内,传动比iHa'才接近于理论值(见图中曲线3)。
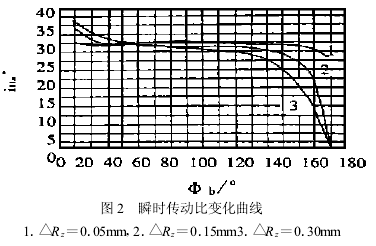
3 结论
在摆线针轮行星传动中,单对齿实际啮合的瞬时传动比在初始啮合段比理论值大,在终了啮合段比理论值小。当加工误差或修正量较大时,单对齿啮合的瞬时传动比由大到小,有较明显的变
化。虽然实际传动是多齿啮合,但由于单对齿啮合传动比的单调递减变化,传动中必然有速度波动,产生扭振和噪声,因而会影响其传动的运动平稳性。
由以上的计算机分析看出,摆线针轮行星减速机的加工制造应严格控制加工公差,以获得较好的运动平稳性。对于摆线轮齿形修正,应根据传动比的变化规律采用合理的修正方式,调整传动比的这种单调递减变化,以获得良好的传动性能。









