基于遗传算法的摆线针轮行星减速器优化设计
摘要:为了解决摆线针轮行星减速器的传动效率低,结构不够紧凑的问题,通过推导其传动效率的公式,并对设计变量和约束条件进行研究,建立了以体积最小、效率最高为目标函数的优化设计数学模型。采用遗传算法,运用MATLAB软件编制遗传优化程序,调用遗传工具箱进行优化。优化设计结果与传统的设计相比,体积减小16.6,效率增加2.06%,优化效果显著,从而为摆线针轮行星减速器优化设计提供一定的理论和方法。
减速器是机械传动中的核心部件,渐开线减速器具有广泛的应用,但有些场合却不能满足使用要求。摆线针轮行星减速器具有体积小、质量轻、传动比范围大、寿命长、精度保持稳定、传动平稳等一系列的优点而得到了广泛的应用。但摆线针轮行星减速器的传动效率却比渐开线行星减速器的传动效率低,因此研究摆线针轮行星减速器的参数设计,优化体积和传动效率具有重要意义。
由于摆线针轮行星减速器涉及的参数比较多,关系比较复杂,影响的因素也较多,这就给摆线针轮行星减速器的优化设计带来了一定的困难。从现在所发表的摆线针轮行星减速器的优化设计论文[1][2]142[3]来看尚存一定的不足,比如目标函数单一,不能有效提高摆线针轮行星减速器的传动效率;各约束条件单位不统一,给优化设计的实现造成了一定的难度。因此全面和深入地研究摆线针轮行星减速器的优化设计问题,对摆线针轮行星减速器技术发展有一定的实用意义。本文中我们推导出摆线针行星减速器传动效率的公式,以体积最小和效率最高作为目标函数,利用遗传算法对摆线针轮行星减速器进行多目标优化设计。
1 摆线针轮减速器优化设计数学模型
1.1 设计变量
摆线针轮传动结构如图1所示。现研究一级摆线针轮行星减速器优化问题,取摆线针轮行星减速器的针轮分布圆直径DZ;针齿销直径dz′;摆线轮宽度B;短幅系数K1;摆线轮内孔直径D1;柱销直径ds′作为设计变量,即
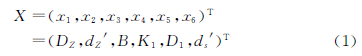
1.2 目标函数
(1)本文以在功率和传动比一定条件下,并选定输出机构销轴数Zs,选择减速器体积最小为目标函 数[2]142,即
minf1(x)=π4(DZ+dZ′+2Δ1)2(2B+δ) (2)
式中,Δ1为针齿套壁厚,一般取Δ1=2~10mm;δ为摆线轮之间的间隔,δ=b-B,b为转臂轴承宽度。
(2)以摆线针轮行星减速器的传动效率为另一个目标函数。
当针轮固定时,转臂输入时(针轮输出时,转臂输入时类似),摆线针轮行星减速器的传动效率η 可近似用下式计算[4]330。
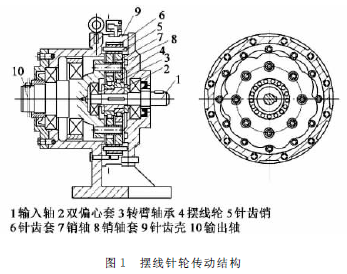
η=ηxcηBηWηB′2 (3)
式中,ηxc为当针轮固定,减速部分的啮合效率,ηxc=1-0.04πZcK1(1-dZ′DZ)1+0.04πK1(1-dZ′DZ);ηB为转臂轴承的效率,其概略值为,ηB=0.99~0.995;ηW为输出机构的效率,ηW =1- 0.08DZK1ds′π[(DZ-dz′-2Δ1-K1DZ/Zb)+D1](d′s+2Δ2);ηB′为输入或输出轴上的滚动轴承的啮合效率,其概略值为ηB′=0.99~0.999。
由文献[4]324-330经整理后,其效率计算式为
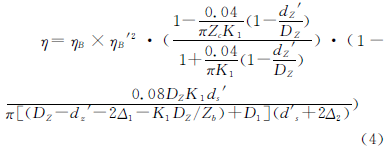
考虑到η∈(0~1),将效率最大值转换成最小值,则效率最大的目标函数是
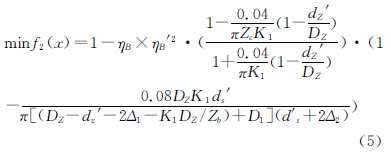
式中,Δ2为柱销套壁厚,一般取Δ2=2.5~5mm;Zb为针轮齿数,Zb=i+1;Zc为摆线轮齿数Zc=i。
1.3 约束条件的建立
(1)摆线轮齿廓不根切条件的约束条件

式中,Ds为柱销孔中心分布圆直径,Ds=dfc+D12;dfc为摆线轮齿根圆直径,dfc=DZ-(dz′+2Δ1)-2 K1RZ/Zb,所以Ds=[DZ-(dz′+2Δ1)-K1DZ/Zb+D1]/2;dsk为销轴孔直径,dsk=ds+2A,ds为销轴套外径,ds=ds′+2Δ2,A 为偏心距A =K1DZ/2Zb,所以dsk=ds′+2Δ2+K1DZ/Zb;Δ′为销轴孔与摆线轮内孔之间所留的一定厚度,Δ′=0.03DZ。
所以推得
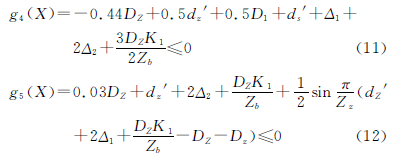
(4)摆线轮与针齿的接触强度条件
由文献[5]74-82推导整理得
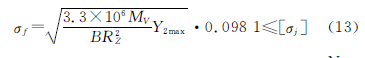
式中,MV为输出轴的阻力矩,MV =97 360ZcNHnH,NH为输入功率(kW);nH为主轴转速(r/min);Y2max为最大接触应力处的位置系数(由文[5]77表10查取);[σj]为许用接触应力(MPa)。得
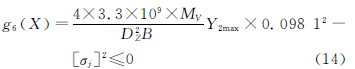
(5)针齿销的弯曲强度条件
对于双支点针齿销的弯曲应力,由文献[5]82-85推导整理得
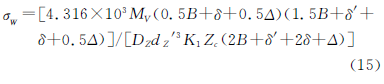
故约束条件为
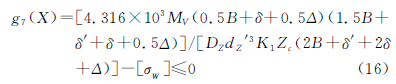
式中,[σW ]为针齿销许用弯曲应力(MPa);δ′为摆线轮于针齿壳侧面见的间隙(mm),一般取δ′=4mm;δ为摆线轮间隔环的厚度(mm),δ=b-B,b为轴承的宽度;Δ为针齿壳侧面的壁厚(mm),一般为B≥Δ≥dZ′。
(6)柱销的弯曲强度限制条件为
W 机构中的柱销所受的最大弯曲应力由文献[5]85-87推导得

(8)短幅系数K 应在0.45~0.8范围选取,即
g10(X)=0.45-K≤0 (21)
g11(X)=K-0.8≤0 (22)
(9)摆线轮壁厚的约束条件[4]318
摆线轮的厚度一般为B=(0.05~0.1)DZ,故
g12(X)=0.05DZ-B≤0 (23)
g13(X)=B-0.1DZ≤0 (24)
综上所述,摆线针轮减速器的多目标优化设计数学模型可表示为
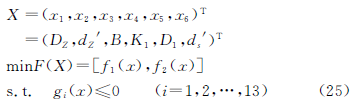
2 遗传优化
由于遗传优化具有鲁棒性好、全局寻优的特点[6],为了避免陷入局部最优解,本文采用遗传算法对摆线针轮行星减速器进行多目标优化设计。
2.1 求解多目标优化问题的遗传算法
遗传优化中为了综合考虑各分目标函数在相对重要程度方面的差异和量纲上的差异,使各个分目标函数能均匀一致地趋向于各自的最优解,采用加权法[7]26。其目标函数表示为
F(x)=w1f1(x)+w2f2(x) (26)
综上所述,摆线针轮行星传动是多目标函数的优化问题。由于体积和效率两目标函数的量纲不同,值的大小相差很大,构造统一目标函数时难以充分反映各子目标函数的重要程度,因此先将体积和效率的目标函数作无量纲处理[8]。由于在摆线针轮行星减速器中体积和效率具有同等的地位,所以我们将各单目标优化值的倒数取作权重系数。
ωi=1/fi*(x)fi*(x)=minfi(x) (27)
式中,ωi是作了无量纲处理后的第i个子目标函数的 权重。
经过这样的处理后,使各子目标函数的量纲得到了统一,在同一量纲的基础上再对各子目标函数赋予相应的权数,最后就将多目标优化转化为了单目标优化。按照此方法,评价函数不仅不会受到各分目标函数值相对大小的影响,还能充分反映出各单目标函数值偏离各自最优值的程度。
2.2 遗传优化算法的实现
本文采用MATLAB 语言编制遗传算法程序[7]26[9],利用MATLAB7.0中的遗传算法工具箱中遗传优化函数ga对摆线针轮行星减速器进行遗传优化。先求得f1(x)、f2(x)分别为单目标函数时的最小值,然后再求多目标的最小值F(x)。
3 优化实例及结果分析
3.1 实例
以某公司生产的B12型减速机为设计实例,减速机的输入额定功率P1=11kW,输入转数n1=1440r/min,传动比i=29,输出机构环形槽数Zs=10,摆线轮和针齿的材料均采用GCr15轴承钢,HRC58~62,许用接触应力[σj]=1 100Ma,许用弯曲应力[σW ]=200MPa。
3.2 优化求解
采用MATLAB 遗传工具箱进行遗传优化,具体步骤如下:
①编写以体积最小为单目标函数的M文件,通过调用遗传优化函数ga,求得最小体积为2 044 181;②编写以效率最高为单目标函数的M文件,通过调用遗传优化函数ga,求得最高效率为95.36%;③编写以体积最小和效率最高为多目标函数的M 文件,如图2所示,其中体积的权重为1/2 044 181,效率的权重为1/ (1-0.953 6);④调用遗传算法主函数ga.m。
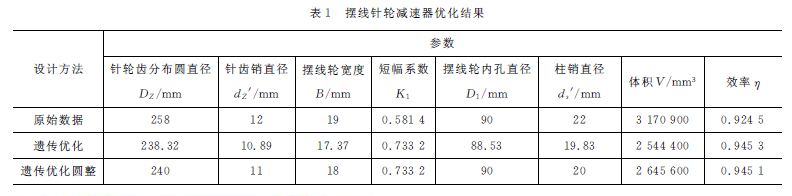
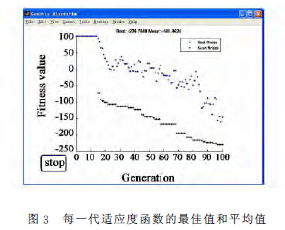
计算结果表明:采用遗传算法优化设计要优于常规设计方法。在保证主要传动元件设计要求的同时,体积减小16.6%,效率增加2.06% 。所以,利用遗传算对摆线针轮行星减速器进行优化设计效果是显著的。
4 结论
分析影响摆线针轮行星减速器的主要参数,建立以体积最小和效率最高为优化设计的目标函数,并系统研究了优化的约束函数。用MATLAB语言编制了遗传算法程序,运用MATLAB遗传工具箱对其进行遗传优化设计,在满足强度条件的前提下,获得比传统方法更好的结果,使其结构更紧凑,传动效率更高。可为摆线针轮行星减速器设计提供理论支撑。









