摆线滚子行星减速机所传递的力矩与功率之间的关系
摘要:摆线滚子行星减速机是继摆线针轮减速机之后出现的又一种新型的减速机。据有关文献报道,这种新型的减速机在日本、美国已经小批量的投产,本文从其传动效率的组成开始,分析了其传动的各基本构件所传递的力矩和功率之间的关系,最后用数学表达式描述了这种关系。
一、摆线滚子行星减速机传动效率的组成
摆线滚子行星减速机是齿差为2的少齿差行星传动,具有与行星齿轮传动的效率完全相同的概念,少齿差行星传动的效率,也是由三部分效率所组成,即为如下三个部分效率之乘积
ηz×ηn×ηm
式中η为总效率,ηz为考虑轴承损失的效率,ηn为考虑啮合损失的效率,ηm为考虑液力损失的效率。其中ηm可以用试验方法确定:首先在全浸油池之中啮合,然后降低油面,使摆线齿轮在油池之外啮合,并测出除液力损失之外的效率ηzn值。则当在油池中啮合时考虑液力损失的效率ηm值由下式确定
ηm=ηηzn
而由于齿廓滑动而产生的啮合损失时的效率和在轴承中所产生的磨擦损失时的效率ηn都可以用较可靠的计算方法确定之。
二、摆线滚子行星传动和基本构件所传递的力矩和功率之间的关系。
此传动的基本构件为转臂H,行星轮g,滚动体b内摆线轮c和输出轴V。作用在各基本构件上的力矩见图1。
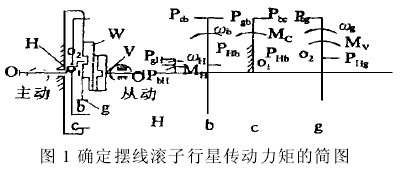
假设在此行星传动中,已知转臂的主动力矩为MH值,并要求确定力矩MV和MC的大小。在此,我们可以运用“力矩法”来求出摆线滚子行星传动中作用在各基本构件上的力矩之间的关系式。大家知道,齿轮的啮合力可以分解为三个分力:圆周力PO,径向力Pr和轴向力Pa。对于摆线齿轮,轴向力为零。另外,在确定力矩的简图(见图1)中,为简化起见,我们省略径向分力,因为径向分力对主轴线的力矩为零。
假设作用在转臂H上的主动力矩MH是顺时针方向,则行星轮g和滚动体b作用于转臂H上的圆周力PgH和PbH向左且有
PgH=MH2e
式中:e———转臂H的O与O1及O1与O2之间的距离。
而转臂H作用在行星轮g上的力PHg向右,当没有磨擦损失时,则
PHg=PgH=MH2e
对于行星轮g,还受有滚动体b的作用力Pbg和构件V的力矩MV(从动力矩)
由∑MK=0,可得
MV=PHg×rg=rg2e.MH(1)
式中:rg———行星轮g的节圆半径。
再由MO2=0, 可得
Pbg=MVrg=MH2e
对于滚动体b,受用行星轮g的作用力Pgb=Pbg和固定内摆线齿轮C的作用力Pcb以及转臂H
的作用力PHb
由∑MO1=0 可得:Pcb×rb=Pgb×rb 所以Pcb=Pgb 再由∑MK=0, 可得:PHb×rb=0 所以PHb=0
因此PbH=0
此式说明转臂H对于滚动体b无作用力,根据作用力与反作用力定律,滚动体b对转臂也无作用力,实际上滚动体b以滚子的纯滚动起到连接内外摆线齿廓的啮合运动的作用。所以对转臂的作用力为零。
对于固定内摆线齿轮C受有滚动体b的作用力
Pbc=Pcb和力矩MC。
且可求得力矩MC的关系式:
MC=Pbc×rc=Pcb×rc=rc×MH2e(2)
式式中:rc———固定内摆线齿轮C的节圆半径。
由图1可清楚地看到,力矩MV与主动力矩MH方向相同;而力矩MC则方向相反,而且它们可以用MH表示,见(1)、(2)式。
现在来进一步找出摆线滚子行星传动各基本构件所传递的力矩与功率之间的关系式。
在均匀速度下运动时,由平衡条件得
MH+MV+MC=0(3)
设nH,nV和nC为构件H,V和C每分钟的转数。当没有磨擦损失时,该传动装置输入和输出的功率的代数和等于零
即MHnH+MVnV+MCnC=0(4)
令NHD,nVD和nCD为构件H、V和C相对于某一构件D(比如机架)而取得的角速度。由(3)和(4)式则得:
所以-MHMV=nVCnHC=1iCHV(7)即作用在各基本构件上带有负号的力矩的比值等于这些构件相对于第三个基本构件的传动比的倒数。
则在没有磨擦损失时的摆线滚子行星传动的效率为:
ηCHV= -NCVNCH= -MVnVCMHnHC= -MVMH1iCHV(8)
公式(6)就是摆线滚子行星传动基本构件所传递的力矩与功率之间的关系式。









