圆柱齿轮热精锻成形载荷影响因素分析
摘要:研究圆柱齿轮热精锻成形载荷计算方法,在圆柱体闭式镦粗计算公式中引入齿形影响因子,得到齿轮热精锻成形载荷经验公式.有限元仿真模拟了模数分别为1,2,3,4mm圆柱直齿轮的热精锻过程,利用仿真得到的成形载荷数据拟合求得了齿形影响因子的计算公式;在该经验公式的基础上分析了锻件齿根圆直径、内孔径、高度、齿轮模数以及坯料材料流动应力对齿轮精锻成形载荷的影响;齿轮热精锻实验和文献中齿轮锻造成形载荷数据共同验证了公式的准确性和适用范围;通过变形的齿轮热精锻成形载荷经验公式,求出不同压力机可锻压齿轮的尺寸范围.
精密锻造具有材料利用率高、节省成本、效率高、产品性能好等优点,但是圆柱齿轮精密锻造成形困难,成形载荷高,设备吨位大[1].为了降低成形载荷,学者们进行了大量研究并有显著成效,如Kondo等[2]将分流减压思想引入齿轮精锻工艺中,Dean等[3]提出浮动凹模结构,刘全坤等[4]使用波形端面冲头,胡成亮等[5]采用两步成形法,均有效降低了齿轮精密锻造成形载荷.日本学者Ohga等[6-8]采用上限分析法计算了成形载荷在成形过程中的变化规律.
虽然上限分析法是一种准确的成形载荷计算方法,但是计算过程复杂繁琐.本文在圆柱体闭式镦粗成形载荷计算公式中引入与相对齿高相关的齿形影响因子,得到齿轮热精锻成形载荷计算经验公式,公式计算准确性高,适用范围广.并通过变形的经验公式,求出不同压力机可锻压齿轮的尺寸范围,对工业生产具有指导性意义.
1 齿轮热精锻成形载荷计算
1.1 齿轮热精锻成形载荷公式
圆柱体闭式镦粗是一种简单、典型的闭式模锻,其成形载荷计算为经典理论[9]:设模腔下角最后充满,则变形区可简化为由半径为ρ、厚度为h 的球面与倾斜自由表面围成的球面体.当从变形区内切取一个微元体时,则作用于该微元体上的应力分别为σθ+dσ,σθ,σr和τ.将作用于微元体上的力在方向列平衡微分方程,利用塑性条件和边界条件,积分并整理得到闭式镦粗至端部尚未出现飞边时的单位压力表达式如下[9].
pz=Cpσs{1+α1D[D/(D-a)-2a/(Da)
]/9a+2(μ-0.25)(H -2b)/R}, (1)
式中:Cp为锻件形状影响因数,按照简单、中等、复杂零件的不同分别取1.0,1.2,1.3~1.4;σs为变形条件下金属的平均流动应力;α1为后充满的下角的变形自由表面与凹模的倾角(径向),α1 =μ1(1.234-0.206a);D 和R 为凹模型腔的直径和半径;μ为坯料与模具接触表面之间的摩擦因数;H为锻件高度;a 和b 分别为锻件下上角隙的轴向和径向未充满值.
对于热精锻,式(1)中的部分参数可以取为常数或者忽略.热模锻锻造温度一般为900~1 100℃,润滑剂采用水基石墨润滑剂,在此温度下摩擦因数取0.3[10-11];假设在热精锻中锻件两端均有1mm圆角未充满,所以未充满值a、b均等于1mm,由此可以求得a1等于0.306;由于未充满值a、b远小于凹模型腔内径D,所以式(1)可以简化为
pz=Cpσs[1+(D-2)/30+0.2(H -2)/D].(2)
成形终了时的成形载荷为
F =pzπ(D-d)2/4, (3)
式中d 为空心锻件内孔直径.
由于在齿轮精锻中,齿形对成形载荷有着很大的影响,实验证明,齿轮精锻的成形载荷大于上式计算结果,所以本文引入一个与齿形大小相关的齿形影响因子Ct.忽略齿形部分对上下冲头产生的轴向锻造力,所以凹模型腔内孔径取齿根圆直径,得到齿轮热精锻终了时的成形载荷公式为
F =Ctpzπ(df-d)2/4, (4)
式中df为齿轮齿根圆直径
1.2 齿形影响因子Ct的确定
齿形影响因子是一个与齿形大小相关的变量,所以定义相对齿高变量来描述齿形大小,为
i=h/Rf=4.5m/df, (5)
式中:h为齿高;Rf为齿根圆半径;m 为齿轮模数.
为了求得齿形影响因子Ct,对4组不同模数齿轮热精锻过程进行了有限元仿真.各组仿真坯料材料均为20CrNiMo,锻造温度为1 000℃,锻件高度为15mm,内孔直径为20mm.仿真计算使用有限元软件DEFORM-3D,设定仿真总步数1 000步,坯
料网格数为30 000,为简化计算,只对一个齿进行仿真.其他仿真参数和计算结果(Ct
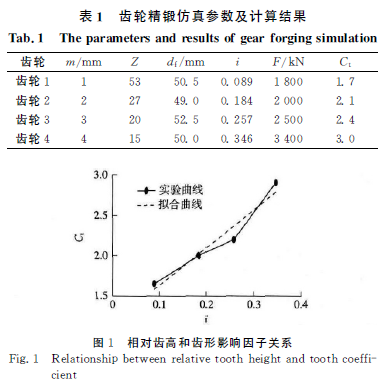
值)如表1所示.图1为表1中相对齿高i和齿形影响因子Ct的关系曲线及拟合曲线.从图中可以看出相对齿高和齿形影响因子Ct几乎成线性关系,对其进行线性拟合,拟合结果为公式(6),拟合度R2 为0.94
Ct=4.69i+1.16. (6)
将式(6)与式(5)联立,可以得到齿形影响因子Ct与齿轮模数m 的关系表达式为
Ct=1.16+21.09m/df, (7)
由式(4)和式(7),可以得到齿轮热精锻成形终了时成形载荷的经验公式为
F=pzπ(df-d)2(1.16+21.09m/df)/4. (8)
2 齿轮热精锻成形载荷影响因素分析
锻件的几何形状、应力状态和齿形大小都会对成形载荷有很大影响.从齿轮热精锻成形载荷经验式(8)中可以看出,成形载荷F 与锻件齿根圆直径df、锻件内孔径d、高度H、齿轮模数以及坯料材料流动应力σs相关.
图2为锻件齿根圆直径、锻件内孔径、锻件高度分别对成形载荷的影响.由图示载荷曲线可以看出,成形载荷随齿根圆直径增大而增大,直径越大,成形载荷增长越快,这是由于锻压的单位变形力和锻件端面投影面积均随齿根圆直径的增加而增加,并且锻件端面投影面积与齿根圆直径成正平方关系;成形载荷随锻件内孔径增大而减小,内径越大,成形载荷减小越快,这是由于锻件端面投影面积与锻件内孔径成负平方关系;成形载荷几乎不受锻件高度的变化影响.
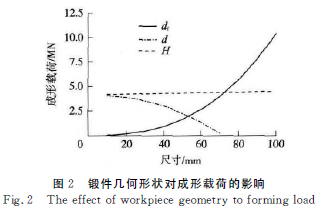
从式(8)中可以看出,成形载荷与材料流动应力成正比.而流动应力与坯料材料、温度及应变速率相关,所以计算成形载荷必须已知锻压条件下坯料材料的流动应力.成形载荷与齿轮模数成线性变化,模数越大,成形载荷越大.
3 齿轮热精锻实验验证
验证实验选取了同步齿轮、齿轮轴热精锻实验(齿轮1和3)和文献[3]中圆柱直齿轮热精锻实验数据(齿轮2),各实验参数如表2所示.齿轮1和3锻造在10MN摩擦压力机上进行,采用水基石墨润滑剂润滑.计算中锻件形状影响因素Cp取1.1,齿轮1和3的材料流动应力σs取180MPa,齿轮2的流动应力σs取220MPa.表3为实验结果和计算结果比较,可以看出,齿轮1和2的计算结果与实验测量载荷误差小于15%;齿轮轴由于相对齿高较大,超出齿形影响因子拟合范围,误差较大,为26%.实验结果说明公式用于齿形影响因子拟合范围内的圆柱直齿轮和斜齿轮热精锻成形载荷计算精度较高,拟合范围外的计算结果仅供考.
4 齿轮热精锻压力机公称压力选取
根据第2章,锻件高度对成形载荷影响不大,所以可以忽略.在式(8)中,H 取52,则简化为
F=pzπ(df-d)2(1.16+21.09m/df)/4, (9)
将上述公式变形为模数与齿根圆直径关系式(10),其他参数取为常量.
m =0.2Fdf/pzπ(df-d)2-0.06. (10)
图3 不同公称压力的压力机可锻压实心齿轮范围
Fig.3 Dimension range of forged solid gears on the presses with different
nominal pressure
对于实心齿轮(d=0),热精锻锻件材料流动应力取180MPa,成形载荷F 分别取6.3,10.0,20.0MN,则可画出3种公称压力下的压力机可锻压的实心齿轮尺寸和模数的选取范围,如图3所示,曲线以下为可选范围.从图中可以看出,模数5mm 的齿轮为例,6.3MN 压力机可成形最大齿根圆直径约62mm的齿轮.
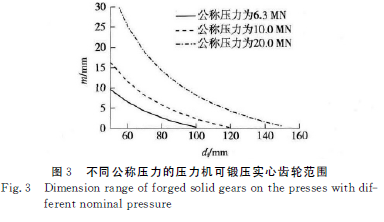
图4表示公称压力为10MN 的压力机在不同坯料材料流动应力下可锻压的实心齿轮尺寸和模数选取范围,图5为10MN压力机成形不同锻件内孔径下可锻压的空心齿轮尺寸和模数选取范围,曲线以下为可选范围
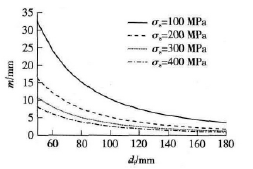
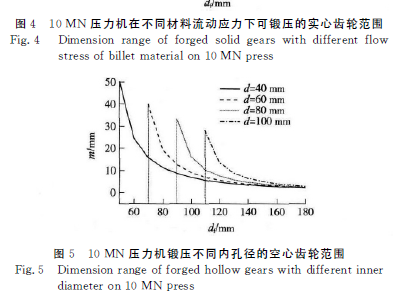
5 结 论
通过拟合修正得到齿轮热精锻成形载荷经验公式.齿轮热精锻实验结果为:同步齿轮和直齿轮成形载荷计算误差小于15%,齿轮轴成形载荷计算误差为26%,实验结果说明公式用于齿形影响因子范围为1.7~3.0的圆柱直齿轮和斜齿轮热精锻成形载荷计算精度较高.
在齿轮热精锻成形载荷随齿轮齿根圆直径、模数、材料流动应力增大而增大,随锻件内孔直径增大而减小,锻件高度对成形载荷影响不大.
通过变形的齿轮热精锻成形载荷经验公式,求出不同压力机可锻压齿轮的尺寸范围,为工业生产提供了指导.









